1、试求点到平面的距离.

　解:设是平面上任意一点，问题等价于距离的最小值.

　约束条件为.

　由此设拉格朗日函数

　　+　

　解方程组

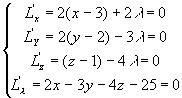
　得唯一驻点 .

　所以，.#

2、设有二阶倒数，且又求证.

　解:因为且连续（因为有二阶倒数）

所以.

并且.

设

则，

所以在定义域上为上凹.

令，得

显然为其极小值点.

而

所以 ，从而.#

3、求.

解：=

= #

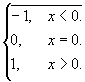4、已知方程的两个根一个比1大，一个比1小，求 的取值范围.

解：设

则，在处取极小值.

由函数性质，只要，就有两个符合给定条件的根.

即求

解之得 .#

5、在的展开式中，常数项是多少？.

解：

而

所以，只有当为偶数，时，得常数项.

所以，=393.#